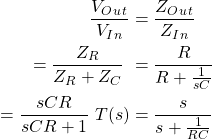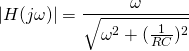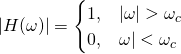内容

“过滤器”这个词意味着它将删除不需要的东西。过滤器的最佳示例是水过滤器。为什么用?它用于去除水中的杂质。电滤清器也与滤水器相同。
电滤清器包含电阻器,电感器,电容器, 和放大器。电滤波器用于通过一定级别的信号频率它将衰减具有较低或高于某个频率的信号。
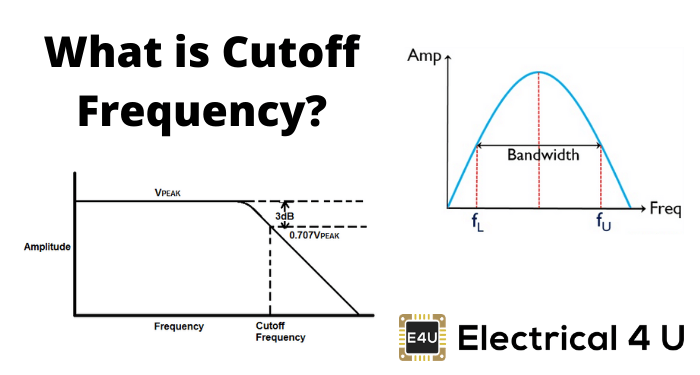
过滤器操作的频率,该频率被称为截止频率。在设计过滤器时设置截止频率。
什么是高通滤波器?
一种高通滤波器(也称为a低剪裁过滤器或者低音剪裁过滤器)电子滤波器是允许具有高于特定截止频率的频率的信号,并衰减具有低于截止频率的频率的信号。
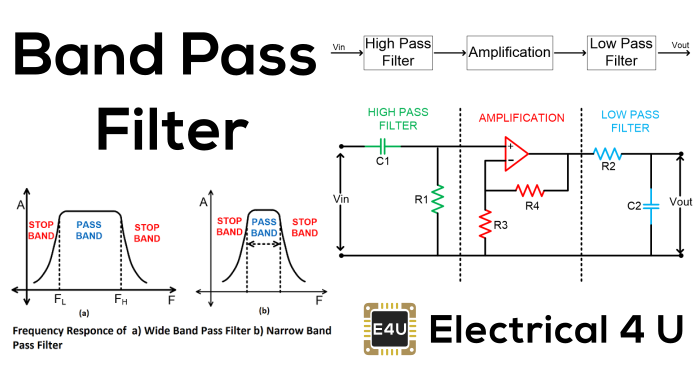
高通滤波器的倒数是一个低通滤波器,这允许具有低于截止频率的频率的信号,并阻止该截止频率高于上方的所有频率。还有乐队通过过滤器,它将高通滤波器和低通滤波器的功能组合到仅允许特定频率范围内的频率。
高通VS低通滤波器
高通滤波器的特性正是低通滤波器的相反特性。差异包括:
| 高通滤波器(HPF) | 低通滤波器(LPF) | |
| 定义 | HPF是一种电滤波器,允许具有比截止频率更高的频率更高的信号。它被称为低切滤器。 | LPF是一种电滤波器,允许具有比截止频率较低的信号。它被称为高切滤器。 |
| 电路图 | 在HPF中,电容器后面是雷带。 | 在LPF中,电阻后跟电容器。 |
| RC滤波器 | 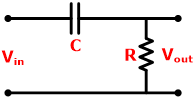 |
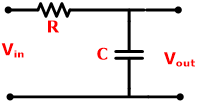 |
| 工作频率 | 高于截止频率 | 低于截止频率。 |
| 重要性 | 从输入信号取消低频噪声非常重要。 | 取消混叠效果非常重要。 |
| 应用程序 | 它以音频放大器,低噪声放大器等放大器使用。 | 它用于通信电路作为抗混叠滤波器。 |
高通滤波器的类型
根据用于制造过滤器的电路设计和组件,有许多类型的高通滤波器。各种类型的高通滤波器包括:
被动高通滤波器
无源滤波器仅由电阻器,电感器和电容器等被动元素组成。它不会使用任何外部电源或放大组件。
被动高通滤波器包括电阻器和电容器(RC)或电阻器和电感器(RL)的组合组成。
有效高通滤波器
有源滤波器是具有运算放大器(OP-AMP)的无源滤波器的组合,或者它包括具有增益控制的放大器。
通过将OP-AMP的反相或非反相组件与无源滤波器连接来制造。
RC高通滤波器
RC滤波器是一种无源滤波器,因为它仅由电容器组成与电阻串联。
高通和低通滤波器的电路图是相同的,只需互换电容器和电阻。RC高通滤波器的电路图如下图所示。
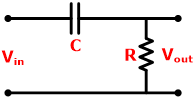
电容器为具有低于截止频率的频率的信号提供非常高的电抗。在这种情况下,电容器充当开关。
电容器为频率高于截止频率的信号提供低电抗。在这种情况下,电容器充当关闭开关。
一阶高通滤波器
一阶高通滤波器仅由一个电容器或电感器组成。这种类型的过滤器有一个转换功能第一个订单。
这意味着如果您在S域中导出了一个方程,则“s”的最大功率是一个。只有使用一个像电感器和电容器等能量存储元件,才有可能。
根据元素的使用,第一订单过滤器可以是活动的或被动的。如果它仅使用活动元素,则它可以是一阶滤波器。RC高通滤波器是一阶无源高通滤波器。
二阶高通滤波器
二阶高通滤波器可以通过级联两阶高通滤波器来得出。因此,它由两个反应部件组成并制造二阶电路。

Stop带中的一阶和二阶滤光斜率的主要区别。二阶滤波器的斜面是一阶滤波器的两倍。

例如,如果我们考虑一阶Butterworth滤波器,则斜坡是+20 dB /十年,并且对于二阶Butterworth滤波器,Slop是+40 dB /十年。
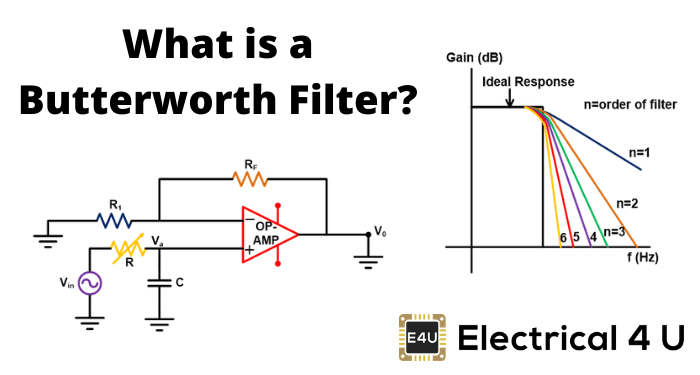
Butterworth高通滤波器
Butterworth滤波器设计成在通带中具有平坦的频率响应。因此,在通过带中,频率响应没有纹波。下图显示了具有频率响应的第一阶和二阶Butterworth高通滤波器的电路图。

Chebyshev高通滤波器
在所有范围的过滤器中,Chebyshev过滤器最小化了实际滤波器和理想过滤器之间的误差。有两种类型的过滤器;类型-i和type-II。I型滤波器称为“Chebyshev滤波器”,并且类型II滤波器称为“venthbyshev滤波器”。

该滤波器响应是波纹和斜率之间的最佳交易。如果纹波设置为0%,则滤波器响应与Butterworth滤波器相同。但是0.5%的涟漪是数字过滤器的良好选择,使尖锐的斜坡。下图显示了Butterworth和Chebyshev滤波器的频率响应差异。

如果在通带存在的纹波,则滤波器称为I型Chebyshev滤波器,如果在停止频段中存在的纹波,则滤波器称为II型反对Chebyshev滤波器。

通带和停止频段之间存在非常快的过渡。但对于这种情况,波纹将存在于通带和停止频段中。这种类型的滤波器称为椭圆滤波器。
贝塞尔过滤器
Butterworth过滤器具有良好的瞬态和幅度行为。Chebyshev过滤器的振幅响应优于Butterworth滤波器,以牺牲瞬态行为为代价。
贝塞尔过滤器具有良好的瞬态响应。但幅度行为很差。Bessel滤波器旨在在通带中获得恒定的组延迟。
被动VS有效高通滤波器
根据电路中使用的组件,滤波器分为两种类型;有源过滤器和无源滤波器。
| 主动过滤器 | 被动过滤器 | |
| 电路元件 | 活动过滤器使用像Op-AMP等活动元素晶体管。 | 无源滤波器使用像电容器和电感等无源元素。 |
| 额外的电源 | 它需要额外的电源。 | 它在信号输入上运行,不需要额外的电源。 |
| 频率限制 | 它具有频率限制。 | 它没有频率限制。 |
| 成本 | 高的 | 成本更低。 |
| 稳定 | 稳定性 | 更好的稳定性 |
| 重量 | 低的 | 高(因为电感的重量非常高) |
| 灵敏度 | 更敏感 | 敏感 |
| Q因子 | 高的 | 非常低 |
| 设计 | 它需要一个复杂的控制系统。因此,该过滤器的设计很复杂。 | 它易于设计。 |
| 效率 | 高的 | 低的 |
| 频率响应特性 | 频率响应特性是尖锐的 | 频率响应特性并不尖锐 |
高通滤波器传递函数方程式
传递函数提供过滤器的数学表示。此数学表达式将输入提供给滤波器的输出行为。
第一阶高通滤波器的传递函数导出在以下等式中。
输出阻抗等于:
输入阻抗等于:
传递函数定义为输出电压与输入电压的比率。
标准形式的转移函数是:
在哪里:
根据该传递函数的较高频率
并且较低的频率
因此,它显示出较低频率的较低频率和最大幅度的零幅度。
截止频率高通滤波器
截止频率被定义为在通带和停止频带之间产生边界的频率。
对于高通滤波器,如果信号频率超过截止频率,则它将允许通过信号。如果信号频率小于截止频率,则它将衰减信号。
截止频率由用户在设计过滤器时定义。对于一阶RC高通滤波器,它表示为以下等式。该等式对于高通以及低通滤波器是相同的。
二阶高通RC滤波器的截止频率由电阻器和电容器决定。它表达为;
从上面的等式,如果R1和R2的值相等,C1和C2的值相同,则表示为“等式”。
高通滤波器BODE绘图或频率响应
频率响应或BODE PLOT.与低通滤波器的频率响应相比,高通滤波器完全相反。
使用传递函数,我们可以绘制滤波器电路的频率响应。高通滤波器的Bode图的幅度曲线和相位曲线如下图所示。

幅度曲线可以通过传递函数的大小获得。
可以通过传递函数的相位等式获得相位曲线。
幅度图
如幅度曲线所示,它将在+20 dB /十年的斜率下衰减低频。从初始点到截止频率的区域称为停止频带。
当它交叉截止频率时,它将允许信号通过。并且截止频率点上方的区域被称为通带。
在截止频率点,输出电压幅度为输入电压的70.7%。
相位图
在截止频率下,输出信号的相位角是+45度。从相位绘图,滤波器的输出响应显示它可以传递到无限频率。但在实践中,输出响应不会延伸到无穷大。
通过正确选择组件,滤波器的频率范围是有限的。
理想的高通滤波器
理想的高通滤波器块块所有具有低于截止频率的频率的信号。它将在通带和停止频段之间立即过渡。
理想高通滤波器的幅度响应如下图所示。幅度将保持为具有比截止频率更高的信号的原始幅度。对于具有比截止频率较低的信号的信号,幅度将完全为零。因此,理想的高通滤波器具有平坦的幅度特性。
理想高通滤波器的传递函数如下面的等式所示:
理想高通滤波器的频率响应特性如下图所示。

实用过滤器无法实现高通滤波器的这种理想特性。但Butterworth滤波器特性非常靠近理想的过滤器。
高通滤波器的应用
高通滤波器的应用包括:
- 它用于放大器,均衡器和扬声器,以降低低频噪声。
- 为了锐化图像,高通滤波器用于图像处理。
- 它用于各种各样的控制系统。