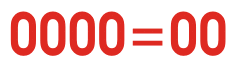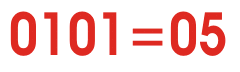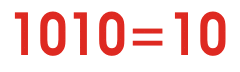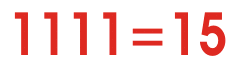二进制数制是什么?
在数字电子技术二进制数字是给出数字输入的最重要工具。在了解之前二进制数字系统我们必须了解我们日常生活中所使用的十进制。人类历史上为计数目的而引入的数字系统。
不同的计数用不同的符号表示。如一个单一的事物被一个符号1计数,如果有两个事物,该符号将为2,如果有三个事物计数,该符号为3。对于4、5、6、7、8、9,十进制中使用的符号分别是4、5、6、7、8和9。符号0(0)表示没有什么可以计数。所以0 1 2 3 4 5 6 7 8 9是10个基本符号用来从0数到9。这就是为什么它被称为十进制或以10为基数的十进制。
但是,如果有超过9个东西要计算,那么我们就不需要另一个新的符号,而是将两个或两个以上的从0到9的符号组合起来,表示大于9的数字。代表9 + 1 = 10,我们用10,代表9 + 2,我们用11,以此类推。就这样,我们建立了十进位数制。
现在来看看二进制数字系统——之所以这样命名是因为它有两个基数(0和1),它们用来表示整个数字系统。看下面的动画来了解二进制到十进制数的转换。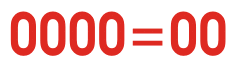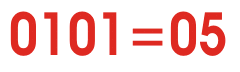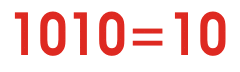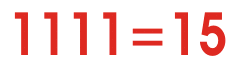
二进制数字系统的历史
b进制是在公元前5 -2世纪由印度学者平加拉引进的。他用长音节和短音节来说明这两种类型的数字,它更像莫尔斯电码。
1679年,戈特弗里德·莱布尼茨发明了现代二进制数字系统,至今仍在使用。
任何一种数(十进制)都可以用二进制数表示。这个系统在数字电子产品中很受欢迎,因为它可以很容易地理解开关模式。
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20. | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30. | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
在上表中,每一个数字都是由任意两个基本符号(0到9)的组合来表示的。这些基本符号称为数字,这些数字在一个被表示的数字中的对应位置称为位。所以上面所有的十进制数都是两位数,双位数。一个数字的最左边的位称为最有效位(MSB),最右边的位称为最不有效位(LSB)。
如果我们观察上面给出的数字,我们会发现前10个连续的数字,即从00到09,在LSB上用改变10个十进制数字来表示。然后MSB被改变为下一个连续的数字,通过改变LSB的数字,其他10个连续的数字(从10到19)被表示出来。在表的第三行,MSB被改变为下一个连续的数字,通过改变LSB的数字,其他10个连续的数字(从20到29)被表示出来。
一共有100个数字,即从00到99个数字用两位十进制表示。100意味着102这意味着(基本数字的数目)的比特数。因此是3位103.或1000年数字(我。e从000到999)可以表示。类似地,n位10n数字可以被表示。
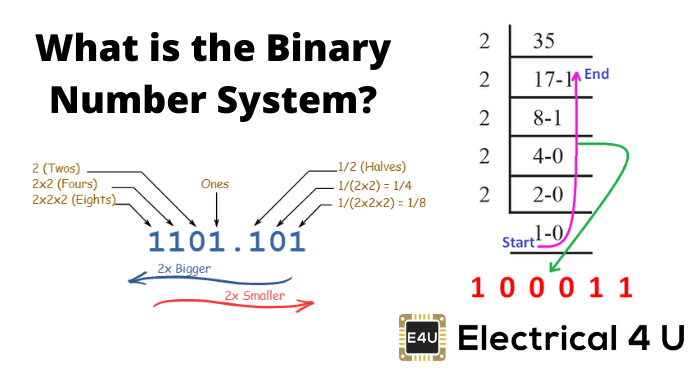
现在考虑一下这种情况,一个数字系统只有两个数字0和1。这个系统也可以用与十进制相同的逻辑来表示。只有两位数字0和1的数字系统称为二进制数字系统。
这里,0用符号“0”表示,1用符号“1”表示,但是如果number大于1,MSB就变成1,通过改变LSB,可以表示另外两个连续的数字。就像十进制一样,二进制所计数的总数取决于它的比特数。
对于二比特二进制,是22数字,即0到3可以表示。公式相同,用二进制数制表示的总数=(基本位数)的比特数。二进制系统的基本数字是2(0和1),但是位数可以从1到无穷任意选择,因此所有的数字范围都可以很容易地用二进制系统表示,就像所有其他的数字系统一样。
二进制数制定义
二进制数制被定义为以2为基数的数制。这意味着这个系统中的数字由两个数字组成- 1和0。
现在,考虑一个十进制数,比如625。从我们能理解的最基本的概念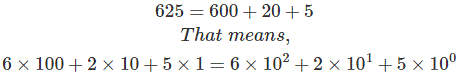
这里,625是三位十进制数,它的最右位或LSB上的数字是5,如果我们从右数位,最右位是0。从右数的下一位是1,这里是第二位,同样的,最左边的位是2,第二位是6。因此,从这个例子中可以清楚地看出,任何小数都可以表示为:
∑数字×10对应位置或位
在上面的表达式中,10是十进制中使用的数字总数,即0到9
与十进制一样,任何数字系统都可以用相同的表达式表示,只有表达式中的10个应该用该系统中使用的数字的总数来代替。因此,任意系统中的任意数,可以表示为:
∑digit×(该系统使用的位数)对应位置或位
二进制数制中使用的位数是2。因此,在本系统中任意数都可以表示为:
∑数字×(2)对应位置或位
| 5 | 4 | 3. | 2 | 1 | 0 | →位置或一些 |
| 1 | 0 | 1 | 0 | 1 | 0 | →二进制数字 |
在这里,二进制数101010号。因此,根据上式,该数可以表示为: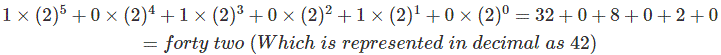
为了更好地了解,请参阅下表:
| 二进制数 | 十进制数 | ||||||||
| 位置 或者一些 |
7 | 6 | 5 | 4 | 3. | 2 | 1 | 0 | |
| 二进制 数字 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+ 0×22+ 0×21+ 0×20= 0 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+ 0×22+ 0×21+1×20= 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+ 0×22+1×21+ 0×20= 2 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+ 0×22+1×21+1×20= 3 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+1×22+ 0×21+ 0×20= 4 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+1×22+ 0×21+1×20= 5 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+1×22+1×21+ 0×20= 6 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0×27+ 0×26+ 0×25+ 0×24+ 0×23.+1×22+1×21+1×20= 7 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0×27+ 0×26+ 0×25+ 0×24+1×23.+ 0×22+ 0×21+ 0×20= 8 | |
查看动画blow,了解不同二进制数是如何计数的